확률분포
1. 이산형 확률 변수
이산형 확률변수는 셀 수 있는 값만을 가지는 확률변수를 말한다.
ex)
- 주사위를 던졌을 때 나오는 눈의 수 {1, 2, 3, 4, 5, 6}
- 동전을 던졌을 때 앞(1) 또는 뒤(0)
특징
- 값이 0, 1, 2 처럼 특정한 값들만 가짐.
- 확률질량함수로 표현
- 각 사건의 확률을 모두 합하면 1이 됨
2. 이산형 확류변수의 종류
ㄱ. 베르누이 확률분포
한 번의 시행에서 결과가 "성공" 또는 "실패"로만 나오는 분포
ex)
- 동전 던지기 (앞/뒤)
- 제품의 합격/불합격
확률질량함수: P(X=x)=p^x (1-p)^(1-x)
기대값: E(X)=p
분산:Var(X)=p(1−p)
ㄴ. 이항분포
베르누이 시행을 n번 독립적으로 반복해서 성공한 횟수를 세는 분포
ex)
- 동전 10번 던져서 앞면이 나오는 횟수
- 공정에서 100개 중 불량품 개수
확률질량함수: P(X=x)=nCx * p^x * (1−p)^(n−x)
기대값: E(X)=np
분산:Var(X)=np(1−p)
ㄷ. 기하분포
첫 번째 성공이 나올 때까지 실패한 횟수 또는 시행 횟수를 세는 분포
- 실패횟수(X) = 성공이 나올 때까지 실패한 횟수
- 시행횟수(Y) = 성공이 나올 때까지의 시행 횟수
ex)
- 주사위 던져서 처음으로 6이 나올 때까지 시도한 횟수
확률질량함수: P(X=x) = (1−p)^x * x
기대값: E(X)=(1-p) / p
분산:Var(X)=(1−p)/p^2
ㄹ. 다항분포
이항분포의 다변량 확장판으로, n번의 시행에서 결과가 k개 이상의 범 주로 나뉘는 경우 각 범주의 개수를 세는 분포
ex)
- 주사위를 10번 던졌을 때 각 눈(1~6)이 나온 횟수
ㅁ. 포아송분포
단위 시간이나 단위 공간에서 어떤 사건이 발생하는 횟수를 나타내는 분포
ex)
- 1시간에 들어오는 고객 수
- 1km 도로에서 발생하는 교통사고 건수
확률질량함수: P(X=x) = λ^k * e^−λ / k!
기대값: E(X)= λ
분산:Var(X)= λ
3. 연속형 확률변수
연속형 확률변수는 어떤 구간 내의 모든 실수값을 취할 수 있는 확률변수를 말한다. 즉 값이 셀 수 없이 무한히 많다
ex)
- 키
- 시간
특징:
- 확률이 특정한 점에서 바로 정의되지 않음: P(X=a)=
- 확률밀도함수(PDF, Probability Density Function)로 표현됨.
- 확률은 구간으로 계산
ㄱ. 균일분포
어떤 구간 [a,b] 내에서 모든 값이 똑같은 확률을 가지는 분포
ex)
- 1~100 사이의 난수를 뽑을 때
확률밀도함수:

기대값: E(X)= a+b/2
분산:Var(X)= (b-a)^2 / 12
ㄴ. 정규분포
평균을 중심으로 대칭적인 종 모양의 곡선. 자연현상과 통계에서 중심적인 역할. 평균이 μ이고 표준편차가 σ인 X의 확률밀도함수
ex)
- 키
- 시험 점수
확률밀도함수:
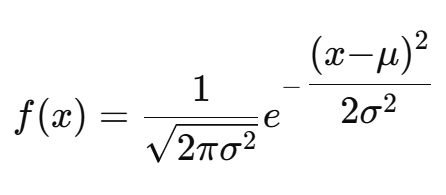
기대값: E(X)= μ
분산:Var(X)= σ^2
ㄷ. 지수분포
어떤 사건이 일어날 때까지의 경과 시간에 대한 연속확률분
ex)
- 물건이 고장 나기까지의 시간
- 콜센터에 다음 전화가 걸려올 때까지의 시간
확률밀도함수:
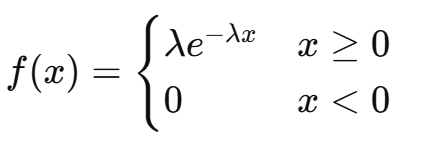
기대값: E(X)= 1 / λ
분산:Var(X)= 1 / λ^2
ㄹ. t-분포
표준정규분포와 같이 편균이 0을 중심으로 좌우가 동일한 분포를 따름. 표본의 크기가 작을 때 평균에 대한 추정에 등장.
두 집단의 평균이 동일한지 알고싶을 때 검정통계량으로 활용
ㅁ. 카이제곱분포
표준정규분포의 제곱합으로 구성. 두 집단 간의 동질성 검정에 활용. 모평균과 모분산이 알려지지 않은 모집단의 모분산에 대한 가설 검정에 사용
ex)
- 분산 검정
- 적합도 검정
기대값: E(X)= ν
분산:Var(X)= 2ν
ㅂ. F-분포
두 집단간의 분산의 동일성 검정에 사용되는 검정 통계량의 분포. 자유도가 2개. 두 개의 카이제곱분포의 비율로 구성되며, 분산의 비율을 비교